Humble introduction to GPT models and PyTorch

In this article I will go through the simplest GPT implementation made by Andrej Karpathy, you can find all the code here. Only prerequisite is to code more or less good in python.

Section 1. Overall structure

When building a GPT model (or any other Neural model) we are going to use the nn module from pytorch library:

import torch.nn as nn

The basic structure of our model will have to look like the following (Meaning you simply copy paste this and then you can add things on top. Later on you'll understand why the super.init is necessary):

class MyModel(nn.Module):
    def __init__(self):
        # Always call parent's init first
        super().__init__()
        # Define layers here
        
    def forward(self, x):
        # Define forward pass
        return x

The reason why we will always inherit the nn.module is because this allows us to create many different building blocks for our model. Actually, the building blocks CAN be (and will be) more things apart from models. For example: layers, activation functions, loss functions, etc.. everything that can make up a model. Then, in our main model, we will include those when initialising it:

class MicroGPT(nn.Module):
    def __init__(self):
        super().__init__()
        self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
        self.position_embedding_table = nn.Embedding(block_size, n_embd)
        self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
        self.ln_f = nn.LayerNorm(n_embd) # final layer norm
        self.lm_head = nn.Linear(n_embd, vocab_size)

Now, simply focus on the bold nn's. The fact that we are assigning to our model some components that inherit the nn module, allows us to get the overall model parameters as follows:

for name, module in model.named_children():
    params = sum(p.numel() for p in module.parameters())
    print(f"{name}: {params/1e6}M parameters")

This will print something like:

token_embedding_table: 0.00416M parameters
position_embedding_table: 0.002048M parameters
blocks: 0.199168M parameters
ln_f: 0.000128M parameters
lm_head: 0.004225M parameters

So, when they say a model has 100M parameters, they mean that the sum of all smaller components of the bigger model, sum up to that amount. Now, if you had forgotten the super().__init__(), it wouldn't track the parameters for that component.

Another important part about this modularization is that now you should more or less understand these scary diagrams:

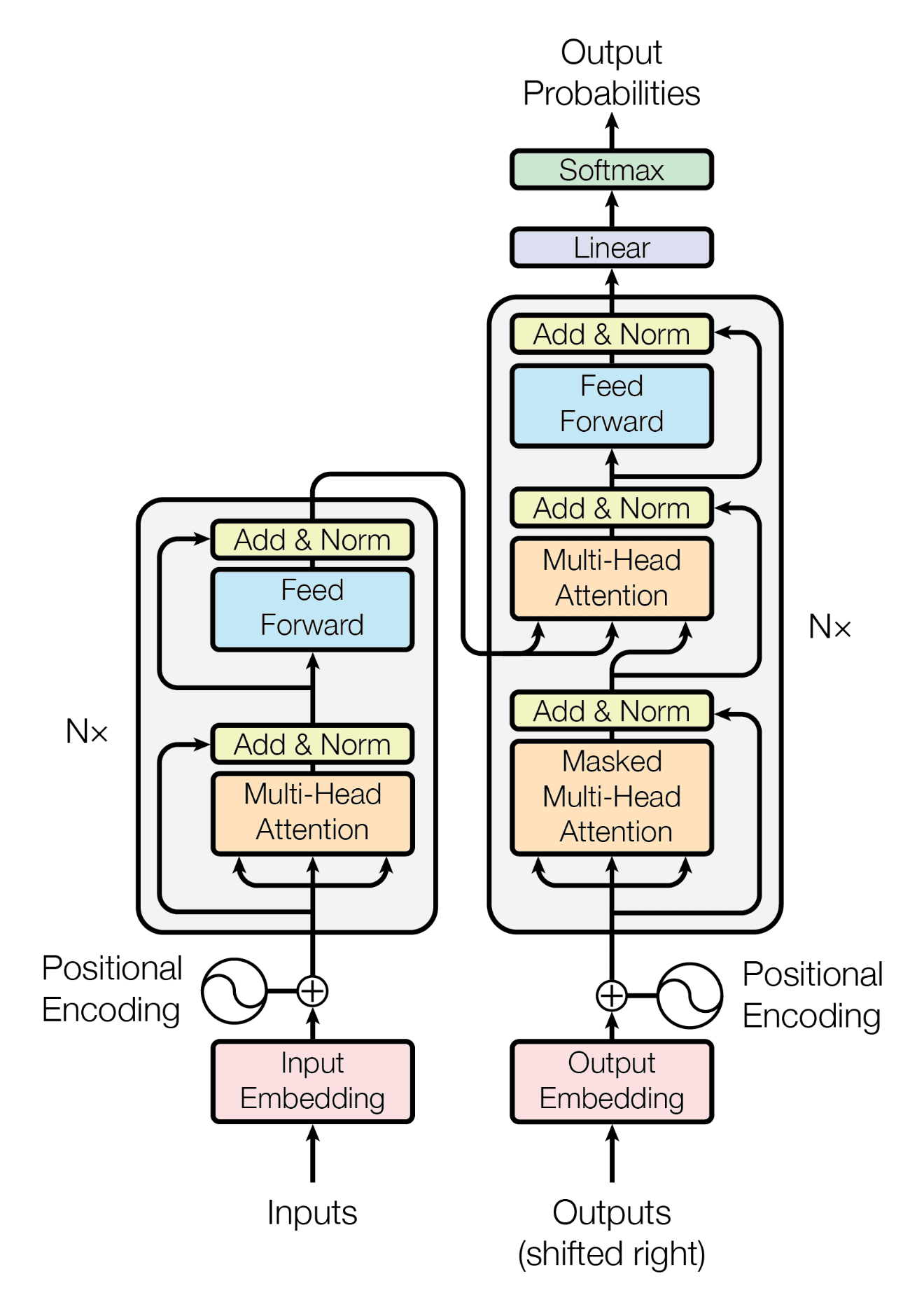
As the caption says, the above diagram shows a representation of the original transformer model, that uses a encoder-decoder architecture, however, GPT models, DONT exactly use this architecture, but rather only the right part (the decoding part). Its architecture looks like this instead:

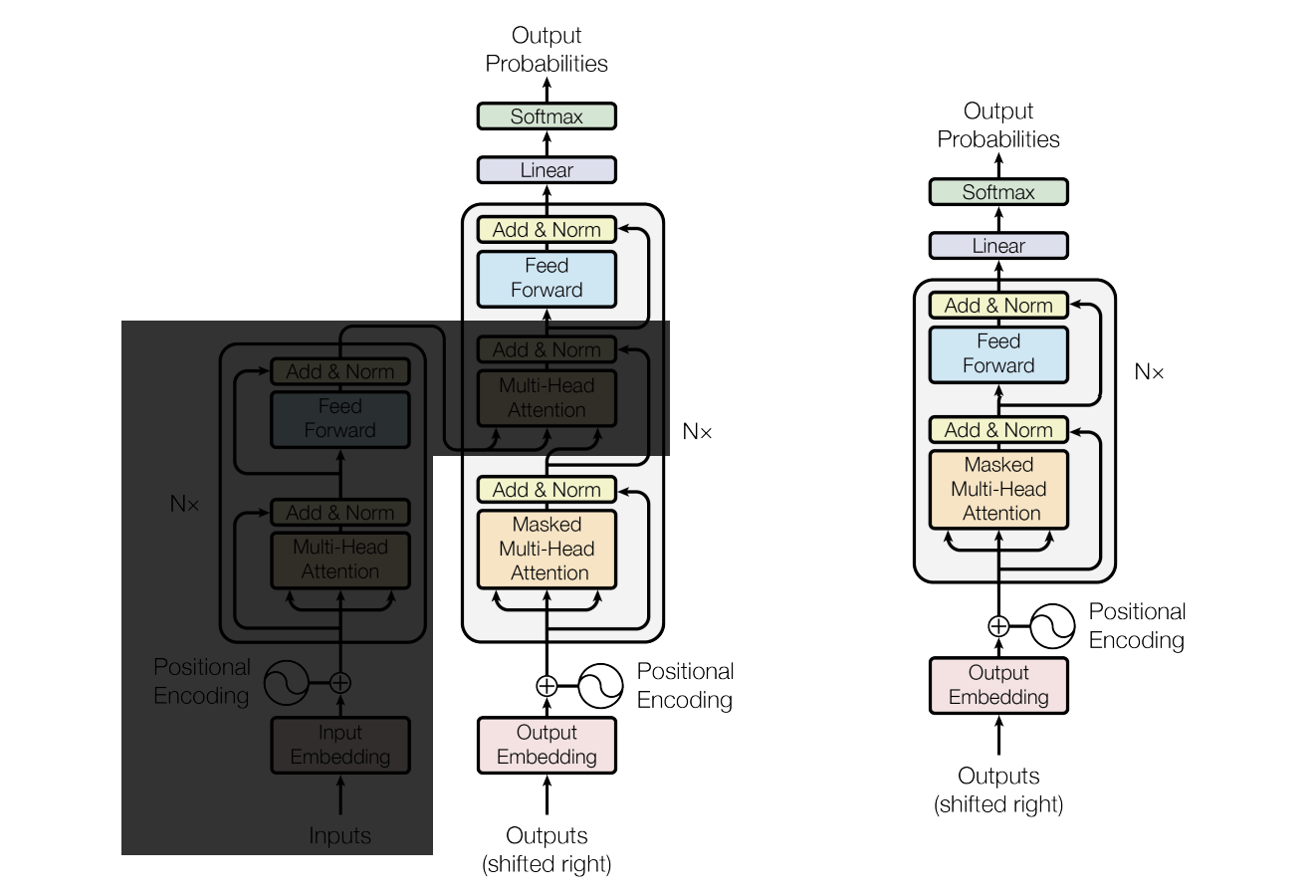
Where the big block with a 'Nx' to the right is the transformer block and its repeated N times. Much better! Another thing we still need to cover is, how to interpret arrows: "What does it mean having a line from Outputs to Output Embedding" or even explaining what the diagram itself represents.

To answer these questions, let's go to the part in the notebook in the 'Full finished code, for reference' block, inside the 'BigramLanguageModel' class (which actually is now a GPT model instead!) I will copy paste the code here:

# Actually its a GPT model not a bigram!
class BigramLanguageModel(nn.Module):

    def __init__(self):
        super().__init__()
        # each token directly reads off the logits for the next token from a lookup table
        self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
        self.position_embedding_table = nn.Embedding(block_size, n_embd)
        self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
        self.ln_f = nn.LayerNorm(n_embd) # final layer norm
        self.lm_head = nn.Linear(n_embd, vocab_size)

    def forward(self, idx, targets=None):
        B, T = idx.shape

        # idx and targets are both (B,T) tensor of integers
        tok_emb = self.token_embedding_table(idx) # (B,T,C)
        pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
        x = tok_emb + pos_emb # (B,T,C)
        x = self.blocks(x) # (B,T,C)
        x = self.ln_f(x) # (B,T,C)
        logits = self.lm_head(x) # (B,T,vocab_size)

        if targets is None:
            loss = None
        else:
            B, T, C = logits.shape
            logits = logits.view(B*T, C)
            targets = targets.view(B*T)
            loss = F.cross_entropy(logits, targets)

        return logits, loss

    def generate(self, idx, max_new_tokens):
        # idx is (B, T) array of indices in the current context
        for _ in range(max_new_tokens):
            # crop idx to the last block_size tokens
            idx_cond = idx[:, -block_size:]
            # get the predictions
            logits, loss = self(idx_cond)
            # focus only on the last time step
            logits = logits[:, -1, :] # becomes (B, C)
            # apply softmax to get probabilities
            probs = F.softmax(logits, dim=-1) # (B, C)
            # sample from the distribution
            idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
            # append sampled index to the running sequence
            idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
        return idx

Okay, there are many things to grasp here. But first, note how the model inhertits the nn.Module and follows the format I showed you in the beggining. The 'generate' method is used to generate new tokens based on the current ones (More on that later).

The 'forward' method is used to pass an input through our model (or component). Note: self(x) is the same as self.forward(x). If we look at the forward method and diagram more closely, we can see that they actually represents the 'path' of the input from the beginning up until generating the logits! We still haven't covered the logits yet, but they are used to get the probabilities of the following words. Note that the code doesn't completely follow the structure but it's stil a valid implementation of the GPT architecture, just organized slightly differently for practical considerations.

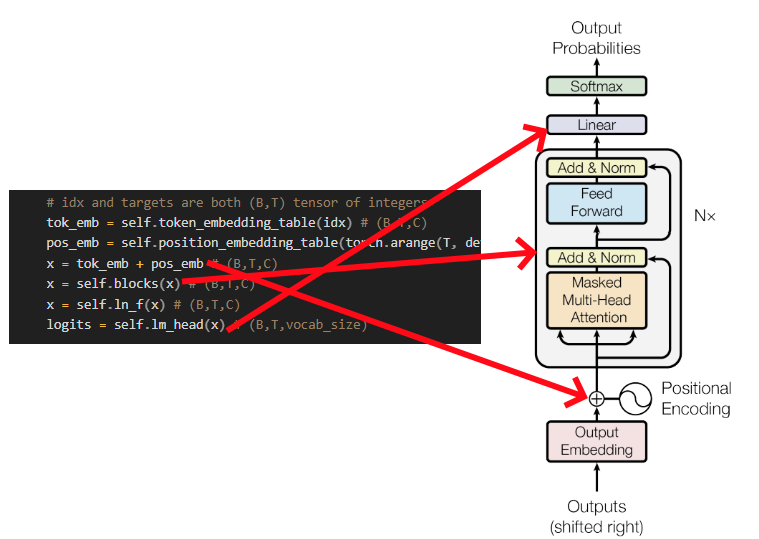
In the following sections, we will go through each component of the model and better understand each part by itself, but by now it should be much easier to go through similar models by yourself!